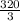Question

determine the steady state temperature distribution between two concentric spheres with radii 1 and 4

Answer 1

Hence, the steady state temperature distribution between concentric spheres with radii 1 and 4 is:

u =
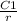`(C1)/(r )` + C2

u =
`((-320)/(3) )/(r)` +
`(320)/(3)`

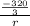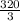
Step-by-step explanation:

Solution:

Note: This question is incomplete and lacks necessary data to solve this question. But I have found a similar question and will try to solve it.

This question has this following part missing:

"If the temperature of the outer sphere is maintained at 80 degrees and the inner sphere at 0 degrees.

Now, this question is complete.

Let's find out the steady state temperature distribution.

As, we know the spherical symmetric heat equation:

`(du)/(dt)` =
`(k)/(r^(2) )`
`(D)/(Dr)` (
`r^(2)`
`(Du)/(Dr)`)

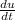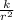
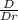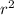
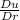Where, small (d) represents the partial differentiation and Capital D represents simple derivative.

And the ordinary differential equation (ODE) for steady state temperature distribution is:

`(k)/(r^(2) )`
`(D)/(Dr)`(
`r^(2)`
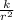
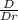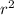
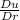`(Du)/(Dr)`) = 0

So it can be said that:

`r^(2)`
`(Du)/(Dr)`

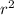
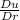
Consequently,

`(Du)/(Dr)` =
`(C1)/(r^(2) )`

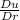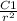
Taking derivative of the above equation we get:

u = -
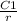`(C1)/(r )` + C2

Solution of the ordinary differential equation

u =
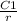`(C1)/(r )` + C2 (Consuming the negative sign into C1 constant)

As, it is given in our question that our boundary conditions are: 1 and 4

So,

Putting the boundary conditions into the variable (r) to find the constants we get:

u1 =
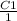`(C1)/(1) }` + C2 = 0 (degrees)

u1 = C1 + C2 = 0 (degrees) equation (1)

Similarly,

u4 =
`(C1)/(4)` + C2 = 80 (degrees)

u4 =
`(C1)/(4)` + C2 = 80 (degrees) equation (2)

Solving for C1, we get:

Equation 1 - Equation 2

(C1 - C2 = 0) - (
`(C1)/(4)` + C2 = 80)

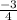`(-3)/(4)`C1 = 80

Solving for C1

C1 = -
`(320)/(3)`

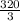
With the help of value of C1, we get value of C2

Put the value of C1 in equation (1) to get value of C2

C1 + C2 = 0

-
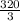`(320)/(3)` + C2 = 0

Solving for C2

C2 =
`(320)/(3)`

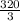
Hence, the steady state temperature distribution between concentric spheres with radii 1 and 4 is:

u =
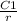`(C1)/(r )` + C2

Plugging in the values of C1 and C2

u =
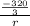`((-320)/(3) )/(r)` +
`(320)/(3)`