Answer:
The number of observations in the data set expected to be between the values 91 and 121 is of 2853.
Explanation:
The Empirical Rule states that, for a normally distributed random variable:
68% of the measures are within 1 standard deviation of the mean.
95% of the measures are within 2 standard deviation of the mean.
99.7% of the measures are within 3 standard deviations of the mean.
In this problem, we have that:
Mean = 101, Standard deviation = 10
Percentage of of observations in the data set expected to be between the values 91 and 121.
91 = 101 - 10
So 91 is one standard deviation below the mean.
121 = 101 + 2*10
So 121 is two standard deviations above the mean
The normal distribution is symmetric, which means that 50% of the measures are below the mean and 50% are above.
Of those 50% below the mean, 68% are between one standard deviation below the mean(91) and the mean(101).
Of those 50% above the mean, 95% are between the mean(101) and two standard deviations above the mean(121).
So the percentage of observations in this interval is of:
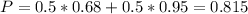
Number of observations in the interval
81.5% of 3500. So
0.815*3500 = 2853
The number of observations in the data set expected to be between the values 91 and 121 is of 2853.