Question

Log base 6 (2x+1) = log base 6 (x-3) + log base 6 (x+5)

Answer 1

We assume you want to find values of x that make the expression true.

Use the rules of logarithms to rewrite as a single log. Then take the antilog and solve the resulting quadratic.


`\log_(6)(2x+1)=\log_(6)(x-3)+\log_(6)(x+5)=\log_(6)((x-3)(x+5))\\\\2x+1=(x-3)(x+5)=x^(2)+2x-15\\\\0=x^(2)-16=(x-4)(x+4)`

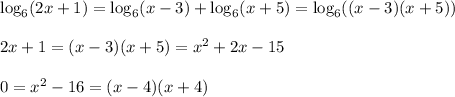
The term
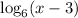
`\log_(6)(x-3)` is only defined for x > 3, so the only solution to this equation is x = 4.