We are given Volume of the larger cylinder is = 1600 cubic centimeters.
Height of the larger cylinder = 16 cm.
We know formula of volume of a cylinder V=
 , where r is the radius of cylinder, h is the height of the cylinder.
, where r is the radius of cylinder, h is the height of the cylinder.
Plugging value of V and h of larger cylinder, we get
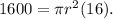
Dividing both sides by 16, we get
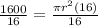
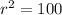
Taking square root on both sides, we get
r=10.
Therefore, radius of the larger cylinder is 10 cm.
We are given cylinders are similar .
Note: The radii and heights of similiar cylinders are in same ratio.
Therefore, we can setup a proportion:
Let us take radius of small cylinder is x.
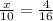
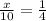
Multiplying both sides by 10, we get
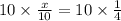
x=2.50.
Therefore, radius of the small cylinder = 2.5 cm.
Now, plugging radius =2.5 and height = 4 in the formula of volume the cylinder, we get
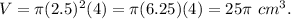
Therefore, correct option is 25 pi cm^3.