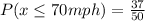Answer:

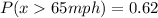

Explanation:
Given
Speed Limits --- States
60 mph ---------- 1
65 mph ----------- 18
70 mph ----------- 18
75 mph ---------- 13
Total -------------- 50
Solving (a): Probability of 60mph or 70mph
This is represented as:
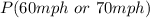
We only consider states with speed limits of 60 and 70mph.
So, we have:
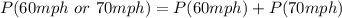
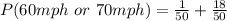
Take L.C.M
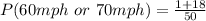


Solving (b): Greater than 65mph
This is represented as:
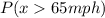
We only consider states with speed limits of 70 and 75mph.
So, we have:
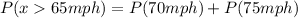
This gives:

Take L.C.M
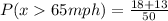
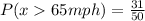
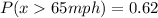
Solving (c): 70mph or less
This is represented as:
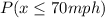
We only consider states with speed limits of 60, 65 and 70mph.
So, we have:
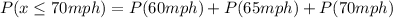
This gives:

Take L.C.M