The larger number is 5.
Step-by-step explanation
Lets assume, the larger number is
 and the smaller number is
and the smaller number is

As the sum of two numbers is 9, so...

Now, the sum of their squares is 41, so....

First, solving equation (1) for
 ....
....
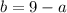
Now, plugging this
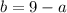 into equation (2) , we will get...
into equation (2) , we will get...

If
 then
then
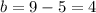
So, the larger number is 5.