Question

The sum of two numbers is 9 and the sum of their squares is 41. What is the larger number?

Answer 1

5 because 5+4 = 9 and 5^2+4^2= 41
Hope this helps!

Answer 2

The larger number is 5.

Step-by-step explanation

Lets assume, the larger number is
`a` and the smaller number is
`b`

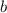
As the sum of two numbers is 9, so...

`a+b= 9 ...............................(1)`

Now, the sum of their squares is 41, so....

`a^2 + b^2 = 41 .......................................(2)`

First, solving equation (1) for
`b`....

`b=9-a`

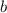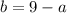
Now, plugging this
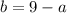`b=9-a` into equation (2) , we will get...

`a^2 +(9-a)^2 = 41\\ \\ a^2 +81-18a+a^2 =41 \\ \\ 2a^2-18a+81 =41 \\ \\ 2a^2-18a+40=0\\ \\ 2(a^2 -9a+20)=0\\ \\ a^2 -9a+20=0\\ \\ (a-5)(a-4)=0\\ \\ a=5,4`

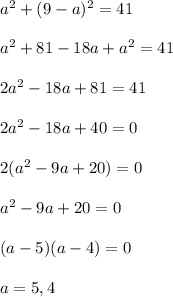
If
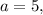`a=5 ,` then
`b=9-5=4`

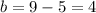
So, the larger number is 5.