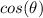Question

PLEASE PLEASE PLEASE HELP!!! Where does the Pythagorean Identity sin2 Θ + cos2 Θ = 1 come from? How 
does it relate to right triangles?

Answer 1

All of the trigonometric functions of an angle θ can be constructed geometrically in terms of a unit circle centered at O. Given that:

Sine function
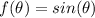
`f(\theta) = sin(\theta)` being
`sin(\theta)= v`
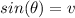
Cosine function
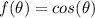
`f(\theta) = cos(\theta)` being
`cos(\theta)= u`

`r = 1`

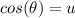
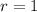
We will demonstrate the identity above. First of all, we need to square each equation, so:


`sin^(2)(\theta)= v^(2)`

`cos^(2)(\theta)=u^(2)`

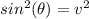
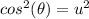
Adding these two equations:


`sin^(2)(\theta)+cos^(2)(\theta)=v ^(2)+u^(2)`

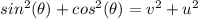
But as shown in the figure, using Pythagorean theorem
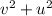
`v^(2)+u^(2)` is always equal to 1, then:


`sin^(2)(\theta)+cos^(2)(\theta)=1`

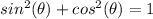
The relation to right triangles is that:

The hypotenuse is always equal to 1
The opposite side is equal to
`sin(\theta)`
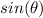
The adjacent side is equal to
`cos(\theta)`