All of the trigonometric functions of an angle θ can be constructed geometrically in terms of a unit circle centered at O. Given that:
Sine function
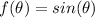
being
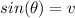
Cosine function
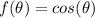
being
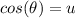
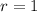
We will demonstrate the identity above. First of all, we need to square each equation, so:
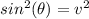
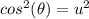
Adding these two equations:
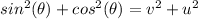
But as shown in the figure, using Pythagorean theorem
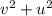
is always equal to 1, then:
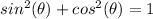
The relation to right triangles is that:
The hypotenuse is always equal to 1
The opposite side is equal to
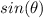
The adjacent side is equal to
