Answer:
D) Δ QRS ~ Δ VTU; 1:4
Explanation:
Given,
In triangle QRS,
QR = 7, RS = 11, and m∠R = 42,
In triangle UVT,
VT = 28, TU = 44 and m∠T = 42
Since,
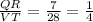

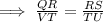
Also, m∠R = m∠T ⇒ ∠R ≅ ∠T
Hence, by SAS similarity postulate,

And, their similarity ratio is 1 : 4,
⇒ Option D is correct.