Answer:
No real solutions, or 0
Step-by-step explanation:
We can determine how many real solutions a quadratic function has, we can use the quadratic formula.
The quadratic formula for expressions written in ax² + bx + c form is:
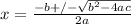
In the equation x² + 5x + 7, a = 1, b = 5 and c = 7
When we plug them in, we get:
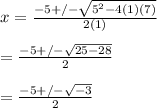
We cannot find the square root of a negative number without diving into the realm of imaginary numbers in which √-3 becomes i√3. Therefore, the equation has no real solutions. This is because the equation x² + 5x + 7 is an upward-facing parabola translated up 7 units and, as such, does not cross the x-axis. If the equation yields a graph that does not cross the x-axis, then there will be zero answers for what variable x equals.