Question

The graph represents the feasible region for the system:

y<=2x
 x + y<=45
x <=30

Minimize the objective function P = 25x + 20y.

The minimum value =?
and occurs when x = ?
and y = ?

Answer 1

The minimum value =

975

and occurs when x =

15

and y =

30

Explanation:

Edge. 2020

Answer 2

We have been given a system of inequalities and an objective function.

The inequalities are given as:

`y\leq 2x\\ x+y\leq 45\\ x\leq 30\\`

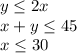
And the objective function is given as:

`P=25x+20y`

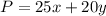
In order to find the minimum value of the objective function at the given feasible region, we need to first graph the region.

The graph of the region is shown below:

From the graph, we can see that corner points of the feasible region are:

(x,y) = (15,30),(30,15) and (30,60).

Now we will evaluate the value of the objective function at each of these corner points and then we will compare which of those values is minimum.

`\text{At (15,30)}\Leftrightarrow P=25\cdot 15+20\cdot 30=975\\ \text{At (30,15)}\Leftrightarrow P=25\cdot 30+20\cdot 15=1050\\ \text{At (30,60)}\Leftrightarrow P=25\cdot 30+20\cdot 60=1950\\`

Hence the minimum value of objective function is 975 and it occurs at x = 15 and y = 30