Question

If (p, q) is the solution to the system of equations, what is the value of q?

−16p − 2q = 100
p − 4q = 200

Answer 1

The solution to the system of equations

• p = 0

• q = -50

Hence, the value of q = -50

Explanation:

Given the system of equations

`\begin{bmatrix}-16p-2q=100\\ p-4q=200\end{bmatrix}`

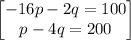
solving to determine the value of q

Multiply p − 4q = 200 by 16:
`16p-64q=3200`

`\begin{bmatrix}-16p-2q=100\\ 16p-64q=3200\end{bmatrix}`

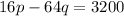
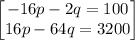
so adding the equations

`16p-64q=3200`

`+`

`\underline{-16p-2q=100}`

`-66q=3300`

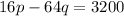
so

`\begin{bmatrix}-16p-2q=100\\ -66q=3300\end{bmatrix}`

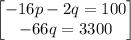
solve -66q = 3300

`-66q=3300`

Divide both sides by -66

`(-66q)/(-66)=(3300)/(-66)`

`q=-50`

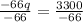
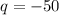
substituting q = -50 in −16p − 2q = 100

`-16p-2\left(-50\right)=100`

`-16p+100=100`

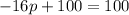
Subtract 100 from both sides

`-16p+100-100=100-100`

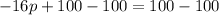
Simplify

`-16p=0`

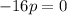
Divide both sides by -16

`(-16p)/(-16)=(0)/(-16)`

`p=0`

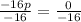
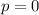
Thus, the solution to the system of equations

• p = 0

• q = -50

Hence, the value of q = -50