Answer:
(D)
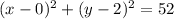
Explanation:
It is given that the endpoints of the diameter of a circle are (−6, 6) and (6, −2).
Now, the standard form equation of the circle is:
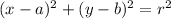
where (a,b) are the coordinates of the center and r is the radius.
In order to find the center, first find the midpoint of the two given points, that is:
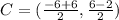
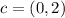
Thus, the center is (0,2).
Now, the radius is the distance from the center to either of the two given points, therefore using distance formula,

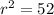
Also, the equation of the circle is:
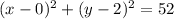
Hence, option D is correct.