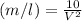Complete Question
The speed of a transverse wave on a string of length L and mass m under T is given by the formula
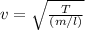
If the maximum tension in the simulation is 10.0 N, what is the linear mass density (m/L) of the string
Answer:
Step-by-step explanation:
From the question we are told that
Speed of a transverse wave given by
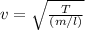
Maximum Tension is
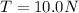
Generally making
 subject from the equation mathematically we have
subject from the equation mathematically we have
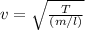
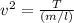
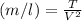
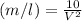
Therefore the Linear mass in terms of Velocity is given by