It's a equilateral triangle. The area of the white region is the area of a sector minus the area of a triangle.
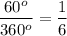
The sector is 1/6 of the circle, therefore the area of the sector is 1/6 of area of the circle.
The formula of an area of the circle:

The area of the sector:

The formula of an area of the equilateral triangle:
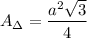

The area of the segment:
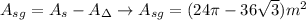
The area of the shaded region:
