1) The half-life is the time required for a substance to reduce to half its initial value. In formulas:
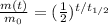
(1)
where
m(t) is the amount of substance left at time t
m0 is the initial mass
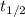
is the half-life
In this problem, the half-life of the substance is 20 years:

therefore, the fraction of sample left after t=40 years will be
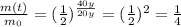
So, only 1/4 of the original sample will be left, which corresponds to 25%.
2) We can use again formula (1), by re-arranging it:

If we use m(t)=10 g (mass of uranium left at time t), and

(the time is equal to 4 half lifes), we get
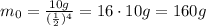
So, the initial sample of uranium was 160 g.