Question

How many positive integers $N$ from 1 to 5000 satisfy both congruences, $N\equiv 5\pmod{12}$ and $N\equiv 11\pmod{13}$?

Answer 1

Use the Chinese remainder theorem. Suppose we set
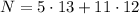
`N=5\cdot13+11\cdot12`. Then clearly taken modulo 12, the second term vanishes, and incidentally
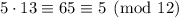
`5\cdot13\equiv65\equiv5\pmod{12}`; taken modulo 13, the first term vanishes, but the second term leaves a remainder of 2. To counter this, we can multiply the second term by the inverse of 12 modulo 13, which is 12 since
`12^2\equiv144\equiv11\cdot13+1\equiv1\pmod{13}`.

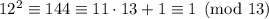
So, we found that
`N=5\cdot13+11\cdot12^2=1649`, but the least positive solution is
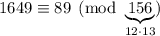
`1649\equiv89\pmod{\underbrace{156}_(12\cdot 13)}`, and in general we can have
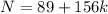
`N=89+156k` for any integer
`k`.

Now, since
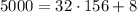
`5000=32\cdot156+8`, or
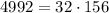
`4992=32\cdot156`, we know that there are 32 possible integers
`N` that satisfy the congruences.