Use the Chinese remainder theorem. Suppose we set
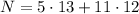
. Then clearly taken modulo 12, the second term vanishes, and incidentally
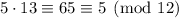
; taken modulo 13, the first term vanishes, but the second term leaves a remainder of 2. To counter this, we can multiply the second term by the inverse of 12 modulo 13, which is 12 since
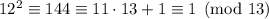
.
So, we found that
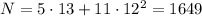
, but the least positive solution is
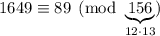
, and in general we can have
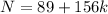
for any integer
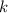
.
Now, since
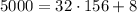
, or
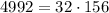
, we know that there are 32 possible integers
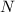
that satisfy the congruences.