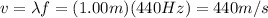Question

A violin string that is 50.0 cm long has a fundamental frequency of 440 Hz. What is the

speed of the waves on this string?

Answer 1

30800 m/s

Step-by-step explanation:

correct answer

Answer 2

For a standing wave on a string, the wavelength is equal to twice the length of the string:

`\lambda=2 L`
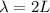
In our problem, L=50.0 cm=0.50 m, therefore the wavelength of the wave is

`\lambda = 2 \cdot 0.50 m = 1.00 m`

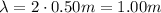
And the speed of the wave is given by the product between the frequency and the wavelength of the wave:

`v=\lambda f = (1.00 m)(440 Hz)=440 m/s`