Question

What are a) the ratio of the perimeter’s b) and the ratio of areas of the larger figure to the smaller figure?

Answer 1

did you get the answers?

Answer 2

a) We have been given two similar figures and we have to find ratio of perimeters of these figures.

Let a be given side of larger figure and b be the given side of smaller figure. Let
`p_(1) \text{ and } p_(2)` be the perimeters of two figures and
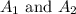`A_(1) \text{ and } A_(2)` be the areas of the two figures.

We know that perimeters of two similar figures are in the ratio of corresponding sides.

`(p_(1))/(p_(2))=(a)/(b)`

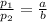
We have been given,
`a=26\text{ and }b=6`

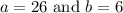
Therefore, upon substituting these values in the above equation, we get

`(p_(1))/(p_(2))=(26)/(6)`

`(p_(1))/(p_(2))=(13)/(3)`

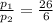
(b)

Further we know that areas of two similar figures are in the ratio of squares of corresponding sides.

`(A_(1))/(A_(2))=(a^(2))/(b^(2))\\ (A_(1))/(A_(2))=(26^(2))/(6^(2))\\ (A_(1))/(A_(2))=(676)/(36)\\ (A_(1))/(A_(2))=(169)/(9)\\`

Therefore, first option is the correct answer.