Question

Given the parent function f(x)=x^2 describe the graph of g(x)=(3x-6)^2+3

a.
expanded vertically by a factor of 3, horizontal shift left 6, vertical shift up 3
c.
compressed horizontally by a factor of 1/3, horizontal shift right 2, vertical shift up 3
b.
expanded horizontally by a factor of 3, horizontal shift left 6, vertical shift up 3
d.
compressed vertically by a factor of 1/3, horizontal shift right 2, vertical shift up 3

Answer 1

For this case we have the following functions transformation:
Vertical expansions:
To graph y = a * f (x)
If a> 1, the graph of y = f (x) is expanded vertically by a factor a.
f1 (x) = (3x) ^ 2
Horizontal translations
Suppose that h> 0
To graph y = f (x-h), move the graph of h units to the right.
f2 (x) = (3x-6) ^ 2
Vertical translations
Suppose that k> 0
To graph y = f (x) + k, move the graph of k units up.
g (x) = (3x-6) ^ 2 + 3
Answer:
expanded horizontally by a factor of 3, horizontal shift rith 6, vertical shift up 3

Answer 2

C. Compressed horizontally by a factor of 1/3, horizontal shift right 2, vertical shift up 3

Explanation:

If a function f(x) is transformed and make f(kx),

f(x) is compressed horizontally by the factor 1/k if k > 1

f(x) is stretched horizontally by the factor 1/k if 0 < k < 1

Also, if f(x) is transformed and make f(x+a),

f(x) is shifted right if a < 0

f(x) is shifted left if a > 0,

Now, if f(x) gives f(x) + k after transformation,

f(x) is shifted vertically k unit up if k > 0,

f(x) is shifted vertically k unit down if k < 0,

Here, the parent function,

`f(x) = x^2`

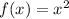
transformed function,

`g(x)=(3x-6)^2+3=(3(x-2))^2+3`

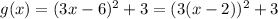
Thus, by the above explanation,

f(x) is compressed horizontally by a factor of 1/3, horizontal shift right 2, vertical shift up 3.

Option C is correct.