Answer:

Step-by-step explanation:
Hello!
In this case, since the radioactive decay equation is:
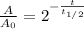
Whereas A stands for the remaining amount of this sample and A0 the initial one. In such a way, since the sample of rutherfordium is reduced to one-third of its nuclei, the following relationship is used:
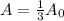
And we plug it in to get:
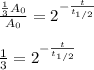
Now, as we know its half-life, we can compute the elapsed time for such loss:
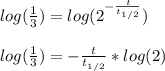

Best regards!