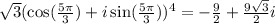Question

Please help!!!

Use DeMoivre's theorem to evaluate the expression

[sqrt 3( cos 5pi/3 + i sin 5pi/3)]^4 ? write the answer in rectangular form


a. 9sqrt3/2 + 9/2 i

b. 9sqrt3/2 - 9/2 i

c. -9/2 - 9sqrt3/2 i

d. -9/2 + 9sqrt3/2 i

Answer 1

Option d -
`\sqrt3(\cos ((5\pi)/(3))+i\sin((5\pi)/(3)))^4=-(9)/(2)+(9\sqrt3)/(2)i`

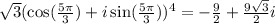
Explanation:

Given :
`\sqrt3(\cos ((5\pi)/(3))+i\sin((5\pi)/(3)))^4`

To find : Use DeMoivre's theorem to evaluate the expression?

Solution :

DeMoivre's theorem state that, for complex number

If
`z = r(\cos\theta+ i\sin \theta)` then
`z^n = r^n(\cos n\theta+ i\sin n\theta)`

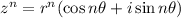
We have given,

`\sqrt3(\cos ((5\pi)/(3))+i\sin((5\pi)/(3)))^4`

On comparing
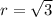`r=\sqrt3` and n=4

Applying DeMoivre's theorem,

`=(\sqrt3)^4(\cos 4((5\pi)/(3))+i\sin4((5\pi)/(3)))`

`=9(\cos ((20\pi)/(3))+i\sin((20\pi)/(3)))`

`=9(\cos (6\pi+(2\pi)/(3))+i\sin(6\pi+(2\pi)/(3)))`

`=9(\cos ((2\pi)/(3))+i\sin((2\pi)/(3)))`

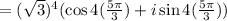
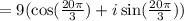
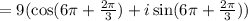
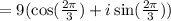
We know, the value of

`\cos ((2\pi)/(3))=-(1)/(2),\sin ((2\pi)/(3))=(\sqrt3)/(2)`

`=9(-(1)/(2)+i(\sqrt3)/(2))`

`=-(9)/(2)+i(9\sqrt3)/(2)`

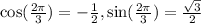
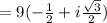
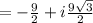
Therefore, Option d is correct.

`\sqrt3(\cos ((5\pi)/(3))+i\sin((5\pi)/(3)))^4=-(9)/(2)+(9\sqrt3)/(2)i`

Answer 2

DeMoivre's theorem

if z = a ( cos θ + i sin θ)
∴ z^n = a^n ( cos nθ + i sin nθ)

For the given complex number ⇒⇒⇒ [ √3 ( cos 5π/3 + i sin 5π/3 ) ]⁴
[ √3 ( cos 5π/3 + i sin 5π/3 ) ]⁴ = (√3)⁴ ( cos 4*5π/3 + i sin 4*5π/3 )
= 9 ( cos 20π/3 + i sin 20π/3 )
= 9 ( cos 2π/3 + i sin 2π/3 )
= 9 ( -1/2 + i √3 /2 )
= -9/2 + 9√3 /2 i

note: 20π/3 = 2π/3 + 6π = 2π/3 + 3 *2π = 2π/3

∴ The correct answer is option d
d. -9/2 + 9sqrt3/2 i