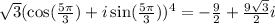Answer:
Option d -
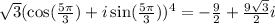
Explanation:
Given :
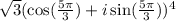
To find : Use DeMoivre's theorem to evaluate the expression?
Solution :
DeMoivre's theorem state that, for complex number
If
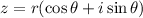 then
then
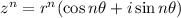
We have given,
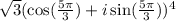
On comparing
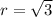 and n=4
and n=4
Applying DeMoivre's theorem,
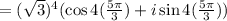
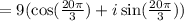
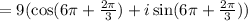
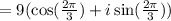
We know, the value of
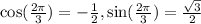
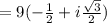
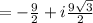
Therefore, Option d is correct.