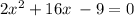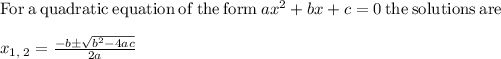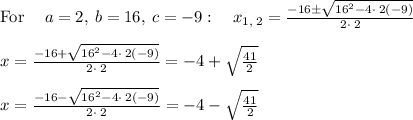Question

What are the zeros of the quadratic function f(x) = 2x2 + 16x – 9?

Answer 1

`2x^(2) +16x - 9 = 0 2(x + 4)^(2) - 41 = 0 (x + 4)^(2) = (41)/(2) x + 4 = \pm \sqrt{(41)/(2)} x = -4 \pm \sqrt{(41)/(2)}`

Answer 2

The zeros to the quadratic equation are:

`x= -4+\sqrt{(41)/(2)}\\\\x= -4-\sqrt{(41)/(2)}`

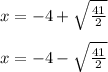
Explanation:

A quadratic function is one of the form
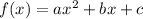`f(x) = ax^2 + bx + c`, where a, b, and c are numbers with a not equal to zero.

The zeros of a quadratic function are the two values of x when
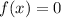`f(x) = 0` or
`ax^2 + bx +c = 0`.

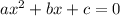To find the zeros of the quadratic function
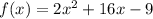`f(x)= 2x^2 + 16x -9` , we set
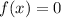`f(x) = 0`, and solve the equation.

`2x^2+16x\:-9=0`

`\mathrm{For\:a\:quadratic\:equation\:of\:the\:form\:}ax^2+bx+c=0\mathrm{\:the\:solutions\:are\:}\\\\x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

`\mathrm{For\:}\quad a=2,\:b=16,\:c=-9:\quad x_(1,\:2)=(-16\pm √(16^2-4\cdot \:2\left(-9\right)))/(2\cdot \:2)\\\\x=(-16+√(16^2-4\cdot \:2\left(-9\right)))/(2\cdot \:2)= -4+\sqrt{(41)/(2)}\\\\x=(-16-√(16^2-4\cdot \:2\left(-9\right)))/(2\cdot \:2)= -4-\sqrt{(41)/(2)}`