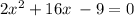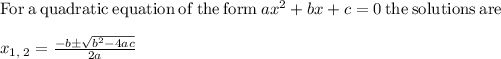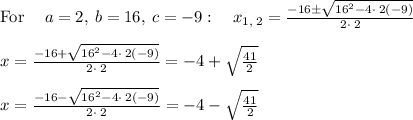Answer:
The zeros to the quadratic equation are:
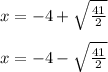
Explanation:
A quadratic function is one of the form
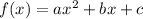 , where a, b, and c are numbers with a not equal to zero.
, where a, b, and c are numbers with a not equal to zero.
The zeros of a quadratic function are the two values of x when
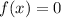 or
or
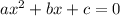 .
.
To find the zeros of the quadratic function
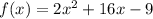 , we set
, we set
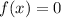 , and solve the equation.
, and solve the equation.