Question

What is the energy q released in the first step of the thorium-232 decay chain? the atomic mass of 232 90th is 232.038054 u and the atomic mass of 228 88ra is 228.0301069 u. express your answer numerically in megaelectron volts?

Answer 1

Answer: The energy released in the given nuclear reaction is 4.98 MeV.

Step-by-step explanation:

The equation for the alpha decay of Th-232 nucleus follows:

`_(90)^(232)\textrm{Th}\rightarrow _(88)^(228)\textrm{Ra}+_(2)^(4)\textrm{He}`

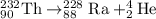
We are given:

Mass of
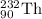`_(90)^(232)\textrm{Th}` = 232.038054 u

Mass of
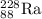`_(88)^(228)\textrm{Ra}` = 228.0301069 u

Mass of
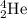`_(2)^(4)\textrm{He}` = 4.002602 u

To calculate the mass defect, we use the equation:

`\Delta m=\text{Mass of reactants}-\text{Mass of products}`

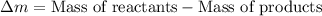
Putting values in above equation, we get:

`\Delta m=(m_(Th))-(m_(Ra)+m_(He))\\\\\Delta m=(232.038054)-(228.0301069+4.002602)=0.0053451u`

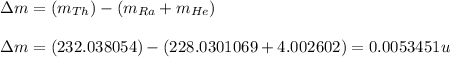
To calculate the energy released, we use the equation:

`E=\Delta mc^2\\E=(0.0053451u)* c^2`

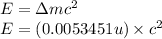
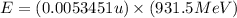`E=(0.0053451u)* (931.5MeV)` (Conversion factor:
`1u=931.5MeV/c^2` )

`E=4.98MeV`

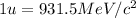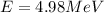
Hence, the energy released in the given nuclear reaction is 4.98 MeV.