Answer: The energy released in the given nuclear reaction is 4.98 MeV.
Step-by-step explanation:
The equation for the alpha decay of Th-232 nucleus follows:
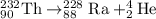
We are given:
Mass of
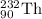 = 232.038054 u
= 232.038054 u
Mass of
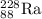 = 228.0301069 u
= 228.0301069 u
Mass of
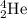 = 4.002602 u
= 4.002602 u
To calculate the mass defect, we use the equation:
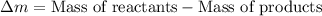
Putting values in above equation, we get:
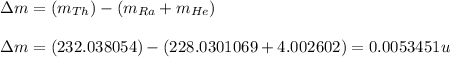
To calculate the energy released, we use the equation:
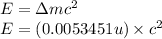
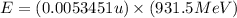 (Conversion factor:
(Conversion factor:
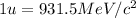 )
)
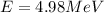
Hence, the energy released in the given nuclear reaction is 4.98 MeV.