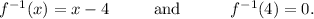Question

Write the inverse function for the function, ƒ(x) = x + 4. Then, find the value of ƒ -1(4). Type your answers in the box.

ƒ -1(x) = _________ x ___________ ______

ƒ -1(4) = _____________

Answer 1

hope you'll understand the workings :)

Answer 2

Answer: The required values are

`f^(-1)(x)=x-4~~~~~~~~\textup{and}~~~~~~~~~f^(-1)(4)=0.`

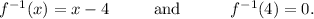
Step-by-step explanation: We are given the following function f(x) :

`f(x)=x+4~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We are to find the values of
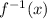`f^(-1)(x)` and
`f^(-1)(4).`

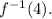
Let us consider that

`y=f(x)~~~~~~~~\Rightarrow x=f^(-1)(y).`

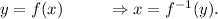
So, from equation (i), we get

`f(x)=x+4\\\\\Rightarrow y=f^(-1)(y)+4\\\\\Rightarrow f^(-1)(y)=y-4\\\\\Rightarrow f^(-1)(x)=x-4.`

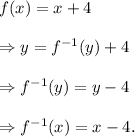
Substituting x = 4 in the above equation, we get

`f^(-1)(4)=4-4=0\\\\\Rightarrow f^(-1)(4)=0.`

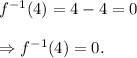
Thus, the required values are

`f^(-1)(x)=x-4~~~~~~~~\textup{and}~~~~~~~~~f^(-1)(4)=0.`