Question

A lab worker monitors the growth of a bacteria colony starting at 9:00 a.m. At that time, there are 100 bacteria. According to the exponential function f(x) = 100(4)x, the bacteria quadruple every hour. Which equation could you use to determine the number of bacteria in the colony after 6 hours?

Answer 1

f(6) = 100(4)6

Explanation:

I took the test

Answer 2

We know that the exponential growth of the Bacteria's population is model by the function
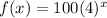
`f(x)=100(4)^x`, so to find the number of bacteria after 6 hours, we just need to evaluate our function at
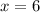
`x=6`. In other words, we are going to replace
`x` with 6 in our function:

`f(x)=100(4)^x`

`f(6)=100(4)^6`

`f(6)=409600`

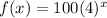
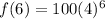
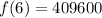
We can conclude that the we should use the equation:
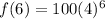
`f(6)=100(4)^6` to find the number of bacteria in the colony after 6 hours. Evaluating the function we get that the number is 409,600.