Question

Please help...

The radius of the planet is 4100 miles. Find the distance d to the horizon that a person can see on a clear day from a height of 1298 feet above the planet. (hint: use the conversion 1 mile = 5280 ft) Round your answer to the nearest 10th, and don't forget to convert feet to miles.

Answer 1

First, we are going to convert 1298 feet to miles. Since we know that 1 mile = 5280 ft, we are going to multiply 1298 ft by
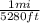
`(1mi)/(5280ft)` to do that:

`1298ft*(1mi)/(5280ft)= (59)/(240) mi`

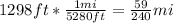
Next, we are going to set up a right triangle using the radius of the Earth and the distance above the planet.
The hypotenuse of our triangle will be the radius of the Earth + the distance above the planet. One of the legs of our triangle will be the radius of the Earth, and the other leg,
`d`, will be the distance that a person will see on a clear day.
Using the Pythagorean theorem:

`d^2= ((984059)/(240) )^2-4100^2`

`d= \sqrt{((984059)/(240) )^2-4100^2}`

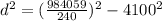
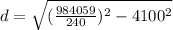
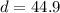`d=44.9` miles

We can conclude that the distance,
`d`, to the horizon that a person can see on a clear day from a height of 1298 feet above the planet is 44.9 miles.