Answer: The standard deviation of the sample will be 11.6.
The standard deviation of the population will be 12.31.
Explanation:
Mr Smith's math class scores : 61, 67, 81, 83, 87, 88, 89, 90, 98, 100
Number of terms,N = 10
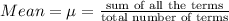
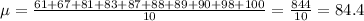
Standard deviation of the sample:
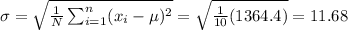
Standard deviation for the population:
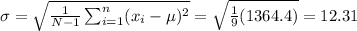
The standard deviation of the sample will be 11.6.
The standard deviation of the population will be 12.31.