Given is a Right triangle ΔACB with angle ∠ACB = 90 degrees.
Given that CD⊥AB, it means we have two Right triangles ΔCDA and ΔCDB.
Given angle ∠ACD = 30 degrees, it means ∠A = 60° and ∠B = 30°
Given side AC = 6 centimeters.
It says to find BD = ?
In Right triangle ΔCDA; CD is adjacent, AC is hypotenuse, ∠ACD = 30°
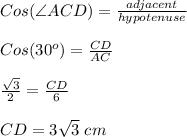
In Right triangle ΔCDB; CD is opposite, BD is adjacent, ∠B = 30°
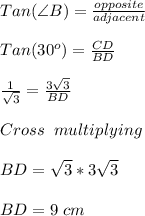
Hence, final answer is BD = 9 centimeters.