For part B, you are correct as far as you've gone. There is no algebraic solution to your equation. A graphing calculator or Newton's Method iteration can get you to a solution fairly quickly.
a ≈ 1.114157141
For part C, you need to consider your answer. For a=0, the equation is that of a straight line, so there is no inflection point at x=1. For cos(a)=0, there are an infinite number of possible values of

that will put a point of inflection at x=1. As you have noted, a=π/2 is only one of them in the range 0 < a < 4.
For part D, again you have stopped part way to the answer. Consider what values of

will make
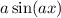
strictly greater than 1. There aren't any. The sine function always crosses zero. This part of the question has no solution.