Question

I am struggling with Parts B and D of this calculus question. I think that Parts A and C are OK. I wonder if Parts B and D require the graph that I drew for Part A?

Answer 1

For part B, you are correct as far as you've gone. There is no algebraic solution to your equation. A graphing calculator or Newton's Method iteration can get you to a solution fairly quickly.
a ≈ 1.114157141

For part C, you need to consider your answer. For a=0, the equation is that of a straight line, so there is no inflection point at x=1. For cos(a)=0, there are an infinite number of possible values of
`a` that will put a point of inflection at x=1. As you have noted, a=π/2 is only one of them in the range 0 < a < 4.


For part D, again you have stopped part way to the answer. Consider what values of
`a` will make
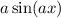
`a \sin(ax)` strictly greater than 1. There aren't any. The sine function always crosses zero. This part of the question has no solution.