Question

A square pyramid has a base with an area of 20 square meters, and its lateral faces have a slant height of x meters. Sydney is constructing a second square pyramid with the same size base, but the lateral faces of her pyramid have a slant height twice as long, 2x. Which statement best describes how the surface area of Sydney’s pyramid compares to the surface area of the original pyramid?

1. Sydney’s pyramid will have the same surface area because the .5 in the expression for the area of the triangular faces will make up for the slant height being doubled.
2. Sydney’s pyramid will have the same surface area because the slant height is not used when finding surface area.
3. Sydney’s pyramid will have a surface area that is exactly double the original pyramid’s because the slant height is used when finding the area of every lateral face.
4. Sydney’s pyramid will have a surface area that is greater than the original pyramid’s but not double the area because the slant height is not used when finding the area of the base.


30 POINTS

Answer 1

Sydney’s pyramid will have a surface area that is greater than the original pyramid’s but not double the area because the slant height is not used when finding the area of the base.

Explanation:

Answer 2

the surface area of a square pyramid with base length b and slant height x is

`A=b^2+2bx`

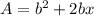
note that b²=base area

so, if we say that her original pyramid's surface area is
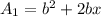
`A_1=b^2+2bx`, then the new one has a slant height of twice that, ie, we replace x with 2x and see what happens

`A_2=b^2+2b(2x)`

`A_2=b^2+4bx`
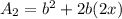
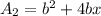
if we try to work
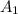
`A_1` back into there

`A_2=b^2+2bx+2bx`

`A_2=(b^2+2bx)+2bx`

`A_2=A_1+2bx`



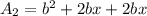
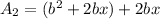
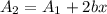
see our options
option 1 is wrong since the surface area increased by 2bx

option 2 is wrong since the surface area increased by 2bx, also we do use the slant height when finding surface area

option 3 is wrong because we got
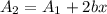
`A_2=A_1+2bx` and not
`A_2=2(A_1)`

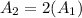
option 4 is correct since the new surface area is greater than the original by 2bx


answer is option 4