since the area of a square is equal to the square of one of its side's length, then the area should be equivalent to

.
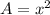
---> equation (1)
By using pythagoras rule which states that the
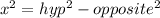
---> equation (2)
where the opposite side's length is 8 and the hypotenuse side's length is 10
by substituting by the values in equation (2) therefore,
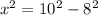
substitute this value in equation (1) then
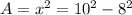
where A is the area of the square whose side is x