Answer:
Option 2, 3 and 5 are correct.
Explanation:
Given question is incomplete, here is the complete question.
The face of a clock is divided into 12 equal parts.
Which statements about the clock are accurate? Select three options.
The central angle formed when one hand points at 1 and the other hand points at 3 is 30°.
The circumference of the clock is approximately 62.8 inches.
The minor arc measure when one hand points at 12 and the other hand points at 4 is 120°.
The length of the major arc between 3 and 10 is approximately 31.4 inches.
The length of the minor arc between 6 and 7 is approximately 5.2 inches.
Option 1. "Central angle when one hand points at 1 and the other hand points at 3."
Since, face of the clock has been divided in 12 equal parts.
So, central angle at the center for each part =
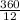
= 30°
Number of parts between 1 and 3 = 3
So central angle between 1 and 3 = 3 × 30°
= 90° (False)
Option 2. "Circumference of the clock = 62.8° inches."
Formula to be used
Circumference = 2πr of a circle
r = radius of the circle
Therefore circumference of he circle = 2π(10)
= 20π
= 62.8 inches (True)
Option 3. "Minor arc measure when one hand points at 12 and the other hand points at 4 is 120°."
Number of parts between 12 and 4 = 4
So Central angle formed = 4 × 30°
= 120° (True)
Option 4. "Length of major are between 3 and 10 = 31.4 inches."
Number of parts between 3 and 10 = 7
Central angle formed by hands = 7 × 30°
= 210°
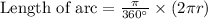
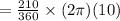
= 39.65 inches (False)
Option 5. "The length of the minor arc between 6 and 7 is approximately 5.2 inches."
Number of parts between 6 and 7 = 1
Central angle between 6 and 7 = 30°
Length of minor arc =

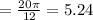
≈ 5.2 inches (True)
Option 2, 3 and 5 are correct.