Question

Witch of the following expression is equivalent to the logarithmic expression below. log(3)5/x^2

A)log(3) 5+2 log(3)x
B)log(3) 5-2 log(3)x
C)2 log(3) 5-log(3)x
D)log(3) 5+log(3)x

Answer 1

assuing you mean

`log_(3)((5)/(x^2))`
remember that
`log((a)/(b))=log(a)-log(b)`
also,
`log(x^m)=(m)log(x)`

so

`log_(3)((5)/(x^2))=`

`log_(3)(5)-log_(3)(x^2)=`

`log_(3)(5)-2log{3}(x)`

the answer is B

Answer 2

Answer: The correct option is

(B)
`\log_35-2\log_3x.`

Step-by-step explanation: We are given to select the expression that is equivalent to the following logarithmic expression :

`E=\log_3(5)/(x^2)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We will be using the following properties of logarithms :

`(i)~\log_a(b)/(c)=\log_ab-\log_ac,\\\\(ii)~\log_ab^c=c\log_ab.`

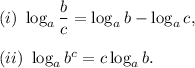
From (i), we get

`E\\\\=\log_3(5)/(x^2)\\\\\\=\log_35-\log_3x^2~~~~~~~~~~~~~~~~~~~~[\textup{Using property (i)}]\\\\\\=\log_35-2\log_3x.~~~~~~~~~~~~~~~~~~~~[\textup{Using property (ii)}]`

Thus, the required equivalent expression is
`\log_35-2\log_3x.`

Option (B) is CORRECT.