Answer: The correct option is
(B)
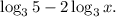
Step-by-step explanation: We are given to select the expression that is equivalent to the following logarithmic expression :

We will be using the following properties of logarithms :
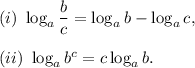
From (i), we get
![E\\\\=\log_3(5)/(x^2)\\\\\\=\log_35-\log_3x^2~~~~~~~~~~~~~~~~~~~~[\textup{Using property (i)}]\\\\\\=\log_35-2\log_3x.~~~~~~~~~~~~~~~~~~~~[\textup{Using property (ii)}]](https://img.qammunity.org/2019/formulas/mathematics/college/29r2zltngoojfoymcx1qjaf83vzpcrg4bn.png)
Thus, the required equivalent expression is
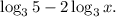
Option (B) is CORRECT.