Answer:
(D) 120 degrees
Explanation:
From the figure drawn, we have
∠ABC=60°
And ∠OAB=∠OCB=90° (angles made by tangent on the circle is 90°)
Thus, ∠AOC+∠OCB∠CBA+∠OAB=360° (Angles sum property of quadrilateral)
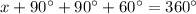
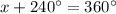
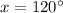
Therefore, the value of x is
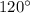
Hence, option D is correct.