We have been given that
mean,
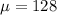
standard deviation
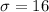
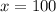
Let us evaluate the z score using the below mentioned formula
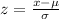
On substituting the given values, we get
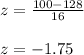
Thus, the value of z is -1.75.
Now, we find the probability that a battery you buy lasts at most 100 hours.
We will find the value for z= -1.75 using the z score table.
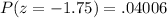
Hence, the required probability is 0.04006