Question

The life of a certain brand of battery is normally distributed, with mean 128 hours and standard deviation 16 hours. what is the probability that a battery you buy lasts at most 100 hours? standardize the variable. x = 100 is equivalent to z =

Answer 1

-1.75 is the answer.

Answer 2

We have been given that

mean,
`\mu = 128`

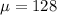
standard deviation
`\sigma = 16`

`x=100`

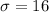
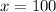
Let us evaluate the z score using the below mentioned formula

`z=(x-\mu)/(\sigma)`

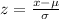
On substituting the given values, we get

`z=(100-128)/(16) \\ \\ z=-1.75`

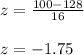
Thus, the value of z is -1.75.

Now, we find the probability that a battery you buy lasts at most 100 hours.

We will find the value for z= -1.75 using the z score table.

`P(z=-1.75)= .04006`

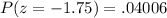
Hence, the required probability is 0.04006