The bus is moving and its initial kinetic energy is

We want the bus to stop, so that its final kinetic energy is zero:
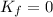
The work-energy theorem states that the work done by an object is equal to its variation of kinetic energy:

Therefore:
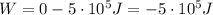
This is the amount of work that needs to be done in order to stop the bus, and its sign is negative because the force applied (the force of the brakes) is opposite to the direction of motion of the bus.