Answer:
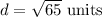
Explanation:
Let
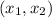 and
and
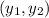 be the two points.
be the two points.
We have to find the distance between the two points.
The distance Formula:
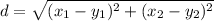
Here, we are given
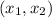 = (5,1) and
= (5,1) and
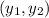 = (9,-6)
= (9,-6)
Then, the distance between these two points is given by:
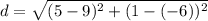
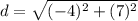
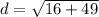
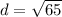
Thus, the distance between the given point is
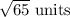 .
.