Answer:
Time taken to reach the ball to the ground is 21 seconds.
Explanation:
Given : A ball is launched into the sky at 272 feet per second from the roof of a skyscraper 1,344 feet tall. The equation for the ball’s height h at time t seconds is
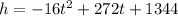 .
.
To find : When will the ball strike the ground?
Solution :
The equation for the ball's height 'h' at time 't' is given by,
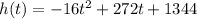
When the ball strike the ground the height of the ball became zero.
Substitute h=0 in the given equation,
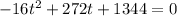
Taking 16 common,

or
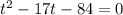
Solve by middle term split,


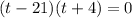
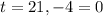
Reject t=-4 as time can never be negative.
Therefore, Time taken to reach the ball to the ground is 21 seconds.