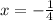Question

A line goes through points (0, 2) and (1, 1). What is the x-coordinate of the intersection of this line with the line y = 3x + 3?

Answer 1

wwd

Explanation:

Answer 2

The x-coordinate of the intersection of the lines is
`x=-(1)/(4)`

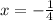
Explanation:

First you need to know the equation of the line that passes through the points (0,2) and (1,1).

The equation of the line in slope intercept form is y=m*x + b

By having two points, you can use them to find the slope m using the expression:

`m=(y2-y1)/(x2-x1)`

In this case (x1,y1)= (0,2) and (x2,y2)= (1,1). Replacing:

`m=(1-2)/(1-0)=(-1)/(1)=-1`

Now you can replace in the values ​​of m, and the values ​​of a point x and y into the equation y = mx + b to find the value of b.

1=(-1)*1 +b

So: 1=-1 +b

b=1+1

b=2

Then you have: y=-1*x +2

So you have the following system of equations:

`\left \{ {{y=-1*x+2} \atop {y=3*x+3}} \right.`

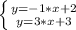
Equating both equations you have:

-1*x+2= 3*x+3

Solving:

-1*x-3*x= 3-2

-4*x= 1

`x=-(1)/(4)`

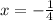
The x-coordinate of the intersection of the lines is
`x=-(1)/(4)`