The exponential term dominates, so that the limit is 0.
To see why: Suppose we take
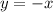
, so that as
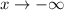
we have
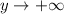
. Now
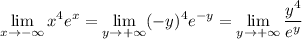
Now recall that for all
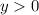
, we have
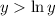
, which means
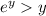
. We can similarly argue that for sufficiently large values of
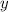
, we have
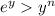
for all integers

. So the denominator in the limit with respect to
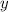
will always (eventually) exceed the numerator and make the entire expression approach 0.