Question

Evaluate (pictured below)

Answer 1

The exponential term dominates, so that the limit is 0.

To see why: Suppose we take
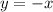
`y=-x`, so that as
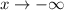
`x\to-\infty` we have
`y\to+\infty`. Now


`\displaystyle\lim_(x\to-\infty)x^4e^x=\lim_(y\to+\infty)(-y)^4e^(-y)=\lim_(y\to+\infty)(y^4)/(e^y)`

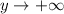
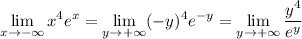
Now recall that for all
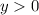
`y>0`, we have
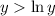
`y>\ln y`, which means
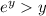
`e^y>y`. We can similarly argue that for sufficiently large values of
`y`, we have
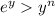
`e^y>y^n` for all integers
`n`. So the denominator in the limit with respect to
`y` will always (eventually) exceed the numerator and make the entire expression approach 0.